Limiti
Quando il campo di esistenza è diverso da tutto R, vi sono delle zone della retta in cui la funzione non e' definita quindi é bene andare a controllare qual'è il valore della funzione in questi punti
Consideriamo la seguente funzione:
\[f(x)= \log x \]
l'argomento di un logaritmo deve essere sempre maggiore di 0, quindi la funzione non è definita per \[x < 0\]
per questo bisogna andare a controllare il valore della funzione in \[x =0\]
per controllare il valore della funzione intorno al punto 0 si usano i limiti
dato che la parte non definita è quella dopo lo zero verifichiamo il valore nell'intorno destro:
\[\lim_{x\to0^+} log(x)\]
e otteniamo che il limite è:
\[-\infty\]
il chè significa che la funzione non esiste dopo lo zero
Dominio
Dominio di una funzione fratta
dato che in matematica la divisione per zero è impossibile, la funzione fratta non può avere come denominatore il numero zero.
\[f(x)=\frac{1}{x-2}\]
il dominio della funzione è quindi l'insieme di tutti i numeri reali eccetto il numero 2,che si scrive:
\[D := \mathbb{R} - \{2\}\]
Perchè:\[ x-2 \ne 0 \] \[ x \ne 2 \]
Dominio di una funzione con logaritmo
Consideriamo la seguente funzione: \[f(x)=\log_{2}x-3\] Poiche' il logaritmo e' definito solo per valori positivi dell'argomento, il termine dentro parentesi dovra' essere maggiore di zero \[x-3>0\] \[x>3\] Quindi il dominio della funzione è: \[D=\{x\in\mathbb{R} | x>3\}\]
Dominio di una funzione con radicale
Consideriamo la seguente funzione: \[f(x)=\sqrt{x-3}\] Poichè la radice è definita solo per valori non negativi del radicando, il termine sotto radice dovra' essere maggiore o uguale a zero \[x-3\geq 0\] \[x\geq 3\] Quindi il dominio della funzione è: \[D=\{x\in\mathbb{R} | x\geq 3\}\]
Al di fuori di questi casi il dominio è l'insieme dei numeri reali. \[D = \mathbb{R}\]Intersezioni
Consideriamo la seguente funzione:
\[f(x)=x^2-2x+1\]
Per trovare l'intersezione con gli assi dobbiamo mettere a sistema con le equazioni degli assi:
nel caso dell'asse y:
\[f(x)= \begin{cases}
x=0 & \\
x^2-2x+1
\end{cases}\]
\[0^2-2*0+1=1\]
Quindi l'intersezione con l'asse y è il punto (0,1)
nel caso dell'asse x:
\[f(x)= \begin{cases}
y=0 & \\
x^2-2x+1
\end{cases}\]
\[x^2-2x+1=0\]
\[(x-1)^2=0\]
\[x-1=0\]
\[x=1\]
Quindi l'intersezione con l'asse x è il punto (1,0)
Derivata
Introduzione
Il concetto di limite, sebbene utilissimo per sostituire ad un punto un intervallo ha comunque dei difetti: infatti applicando il concetto di limite ad un punto io posso avere solamente una visione locale di una funzione: e' come se volessi studiare una strada di notte approfittando della luce di qualche lampione: potro' vedere in quel punto e nelle vicinanze di quel punto ma se voglio sapere cosa succede un po' piu' in la' dovro' avere un altro lampione. A noi serve qualcosa che ci permetta di vedere la funzione nella sua interezza e quel qualcosa sara' la derivata;
Definizione di derivata di una funzione
Per definire la derivata bisogna prima però capire cos'è una derivata; La derivata è il limite del rapporto incrementale \[f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\]
Il rapporto incrementale
La formula completa è
\[\frac{f(x+h)-f(x)}{h}\]
\[f(x+h)-f(x) \quad \text{è differenza tra ordinate}\]
\[(x_0+h)-x_0=h \quad \text{è differenza tra ascisse} \]
come risultato otteniamo il cofficente angolare della retta secante la funzione,quindi il rapporto incrementale ci permette di capire l'andamento della funzione in base al valore del coefficiente angolare della retta tangente alla funzione
Simulazione grafica calcolo rapporto incrementale
Quindi in conclusione se il limite del rapporto inrementale con h\(\to0\) è positivo allora la funzione sta "salendo" e se invece è negativo allora la funzione sta "scendendo"
La formula sopra citata é per un calcolo "generale", per trovare la derivata di una funzione in un punto semplicemente si sostituisce la x con il valore richiesto
Significato geometrico della derivata
La derivata di una funzione in un punto corrisponde al coefficiente angolare della retta tangente alla funzione in quel punto
Derivate fondamentali
| Funzione | Derivata |
|---|---|
| \[f(x)=costante\] | \[f'(x)=0\] |
| \[f(x)=x\] | \[f'(x)=1\] |
| \[f(x)=x^n\] | \[f'(x)=nx^{n-1}\] |
| \[f(x)=sen(x)\] | \[f'(x)=cos(x)\] |
| \[f(x)=cos(x)\] | \[f'(x)= -sen(x)\] |
| \[f(x)=e^x\] | \[f'(x)=e^x\] |
| \[f(x)=ln(x)\] | \[f'(x)=\frac{1}{x}\] |
| \[f(x)=|x|\] | \[f'(x)=\frac{|x|}{x}\] |
Segno
Si deve porre la funzione maggiore di zero e trovare per quali valori di x e' verificata:
per tali valori il grafico sara' sopra l'asse delle ascisse mentre per valori diversi sara' sotto.
Consideriamo la seguente funzione:
\[f(x)=x+4\]
Per trovare il segno della funzione dobbiamo porla a:
\[x+4 > 0\]
\[x>-4\]
Quindi per tutti i valori di x maggiori di -4 la funzione sarà positiva
Operazioni
Derivata somma
\[f(x)=g(x)+h(x) \qquad \Rightarrow \qquad f'(x)=g'(x)+h'(x)\] Un esempio pratico: \[f(x)=x^2+2x+1 \qquad \Rightarrow \qquad f'(x)=2x+2\]
Derivata prodotto
\[f(x)=g(x)h(x) \qquad \Rightarrow \qquad f'(x)=g'(x)h(x)+g(x)h'(x)\] Un esempio pratico: \[f(x)=x^2+2x+1 \qquad \Rightarrow \qquad f'(x)=2x+2\]
Derivata quoziente
\[f(x)=\frac{g(x)}{h(x)} \qquad \Rightarrow \qquad f'(x)=\frac{g'(x)h(x)-g(x)h'(x)}{h^2(x)}\] Un esempio pratico: \[f(x)=\frac{x^2+2x+1}{x^2+1} \qquad \Rightarrow \qquad f'(x)=\frac{2x+2}{x^2+1}-\frac{2x^2+2x+1}{(x^2+1)^2}\]
Derivata potenza
\[f(x)=g(x)^n \qquad \Rightarrow \qquad f'(x)=n\cdot g(x)^{n-1}\cdot g'(x)\] Un esempio pratico: \[f(x)=(x^2+2x+1)^2 \qquad \Rightarrow \qquad f'(x)=2(x^2+2x+1)(2x+2)\]
Derivata funzione composta
\[f(x)=g(h(x)) \qquad \Rightarrow \qquad f'(x)=g'(h(x))\cdot h'(x)\] Un esempio pratico: \[f(x)=sen(x^2+2x+1) \qquad \Rightarrow \qquad f'(x)=cos(x^2+2x+1)(2x+2)\]
Asintoti
Asintoto verticale
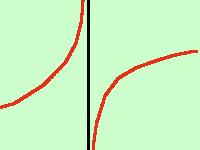
abbiamo un asintoto verticale quando il limite tendente agli estremi del campo di esistenza è uguale a infinito quindi: \[\lim_{x\to x_0^\pm}f(x)=\pm\infty\]
Asintoto orizzontale
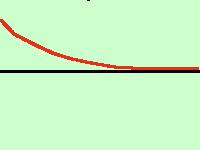
l'asintoto orizzontale è composto da asintoto verticale destro e sinistro, per questo per trovarlo facciamo il limite tendente a +∞ e -∞ e se il risultato è finito allora abbiamo un asintoto orizzontale in quel punto;
è anche possibile che ci sia solo la parte destro o solo sinistra
quindi se:
\[\lim_{x\to\pm\infty}f(x)=k\]
dove k è un numero reale allora abbiamo un asintoto orizzontale in k
Asintoto obliquo
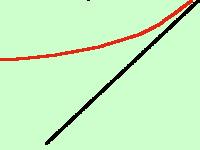
dobbiamo controllare se abbiamo un asintoto obliquo se non abbiamo un asintoto orizzontale(quindi quando il risultato del limite è \(\pm\infty\))
in questo caso dobbiamo trovare prima la m: \[\lim_{x\to\pm\infty}\frac{f(x)}{x}\] se il risultato è \(\neq0\) allora calcoliamo la q: \[\lim_{x\to\pm\infty}f(x)-mx\]
alla fine otteniamo l'equazione della retta dell'asintoto obliquo: \[y=mx+q\]
Studio del comportamento della derivata
Crescenza
Per vedere la direzione della derivata basta vedere il suo segno, se è positivo la funzione cresce, se è negativo la funzione decresce
Consideriamo la seguente derivata:
\[f'(x)=x^2+2x+1\]
Per vedere la direszione della derivata basta vedere il suo segno, se è positivo la funzione cresce, se è negativo la funzione decresce
\[x^2+2x+1>0\]
\[(x+1)^2>0\]
\[x+1>0\]
\[x>-1\]
quindi la funzione cresce per x>-1
Decrescenza
Per vedere la decrescenza considerando la derivata di prima basta porre a \[x^2+2x+1<0\]
Massimo e minimo
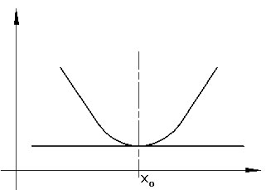
Punto di massimo relativo
Un punto di massimo relativo sara' un punto dove la funzione smette di salire e comincia a scendere;
Matematicamente dovremo dire che quel punto e' piu' alto, cioe' il suo valore e' superiore a quello degli altri
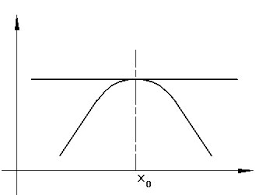
Praticamente per vedere se un punto e' un massimo relativo basta vedere se:
\[f(x_0)\geq f'(x)\]
Punto di minimo relativo
Un punto di minimo relativo sara' un punto dove la funzione smette di scendere e comincia a salire;
Matematicamente dovremo dire che quel punto e' piu' basso, cioe' il suo valore e' inferiore a quello degli altri
Praticamente per vedere se un punto e' un minimo relativo basta vedere se:
\[f(x_0)\leq f'(x)\]
Derivata seconda
Cos'è la derivata seconda?
La derivata seconda è la derivata della derivata primaPerchè è importante?
La derivata seconda ci dice se la funzione è concava verso l'alto o verso il basso e anche i punti di flessoCome si calcola?
La derivata seconda si calcola come la derivata primaCome la usiamo?
Per trovare i punti di flesso e per vedere se la funzione è concava verso l'alto o verso il basso dobbiamo porre la derivata seconda <0,
dopo averlo fatto vediamo per quali valori la derivata seconda è <0 e per quali è >0,
in corrispondenaza dei punti dove la derivata cambia segno avremo un punto di flesso
Flessi
Perchè è importante?
I punti di flesso ci dicono dove/se la concavità della funzione cambiaCome si calcola?
Per trovare i punti di flesso dobbiamo porre la derivata seconda <0, dopo averlo fatto vediamo per quali valori la derivata seconda è <0 e per quali è >0,in corrispondenaza dei punti dove la derivata cambia segno avremo un punto di flesso
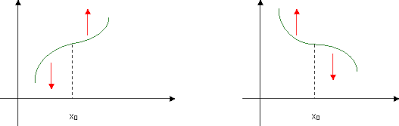
Flesso ascendente
è un punto di flesso dove la derivata seconda passa da - a +
Flesso discendente
è un punto di flesso dove la derivata seconda passa da + a -
Grafico
Consideriamo la funzione: \[f(x)=\frac{x^3-2x}{3}\]
Dominio
il dominio è \[x\in\mathbb{R}\]
Segno
il segno del numeratore:
\[N>0 x^3-2x>0 \]
\[x(x^2-2)>0\quad \to \quad x>0\]
\[x^2-2>0\]
\[x^2>2\quad\to\quad x>+\sqrt{2} \quad and \quad x<-\sqrt{2}\]
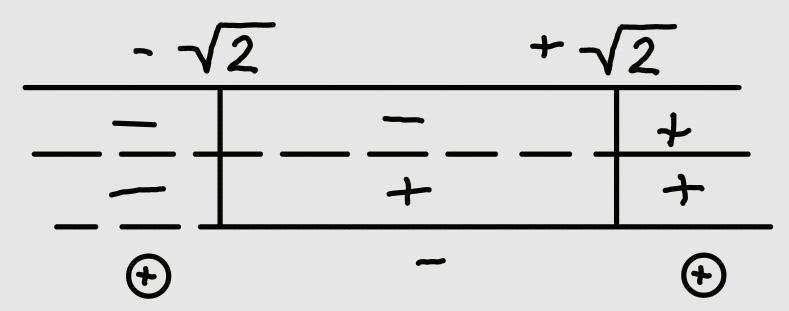
abbiamo che il numeratore è positivo per \[x< -\sqrt{2}\] \[x>\sqrt{2}\]
il del denominatore è sempre positivo in conclusione quindi la funzione è positiva per:
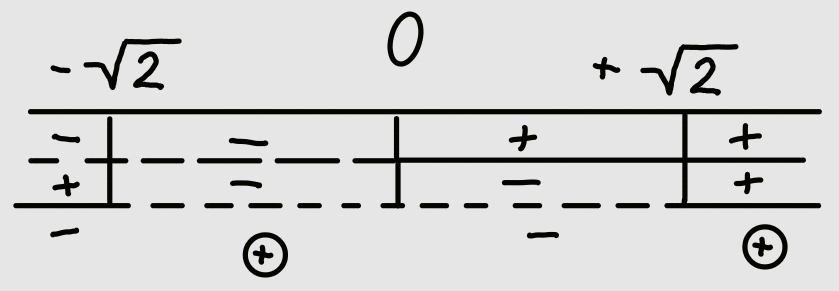
cioè per \[-\sqrt{2}< x < 0\] \[x>\sqrt{2}\]
Intersezioni
Intersezione con l'asse y:
\begin{cases}
x^3-2x\\
x=0\\
\end{cases}
Intersezione con l'asse x:
\begin{cases}
x^3-2x\\
y=0\\
\end{cases}
\begin{cases}
x^3-2x=0\\
x(x^2-2)=0 \quad \to \quad x=0\\
x^2-2=0\\
x^2=2 \quad \to \quad x=\pm\sqrt{2}\\
\end{cases}
Quindi abbiamo che la funzione interseca l'asse y nel punto
(0,0)
e l'asse x nei punti
(0,0)
\((+\sqrt{2},0)\)
\((-\sqrt{2},0)\)
Asintoti
Quando facendo il colcolo del dominio troviamo dei valori per i quali la funzione non è definita, é opportuno vedere se in quei punti è presente un asintoto;
nel nosto caso possiamo saltare il calcolo degli asintoti perchè la funzione è definita per tutti i valori di x